［040］ 続々々・文字の並べ替えと回文

「都会ってカラスてナイス」とか言ってから捨てな椅子。

［とかいってからすてないすとかいってからすてないす］（非回文）

文字の並べ替えネタだけであと5回くらい記事が書けそうな雰囲気ですが、読み続けてくれている方がどのくらいいるのだか大いに心配ですので、最後に2つのトピックをまとめて記して、終わりとしたいと思いますよ。

(1) 複数の並べ替えと転文

ここまで主に取り上げてきた言葉遊びは、回文も畳文も縦横文も、文字の並べ替えが何か1つ与えられたときに、それで変わらない文字列を考えるものでした。

でも［037］で述べたように、並べ替えの個数が1つである必要はありません。たとえば「畳回文」というのは、回文を定義する文字の並べ替え p と、畳文を定義する文字の並べ替え q のいずれでも変わらない文字列のことでした。同様に、「SATOR陣」と呼ばれているものは、正方形の縦横文（左縦書き）を定義する並べ替え s（［038］参照）と、回文を定義する並べ替え p の両方で変わらない文字列です。

これらの並べ替えの組み合わせは何でもいいので、いくらでも新しい言葉遊びができます。縦横文の並べ替え s と、畳文の並べ替え q とで変わらない文字列（いわば「SATOR畳文」）を作ってみたのが上記の「「都会ってカラスてナイス」とか言ってから捨てな椅子」という謎の文でした。

とかいって
からすてな
いすとかい
ってからす
てないす□

25字だと畳文が作れないので、右下を1マス削って24字にしています。


さてここからが本題です。［037］で述べたように、並べ替え t が1つ与えられると、t で移り合う文字列の組（「t(x)＝y」となる文字列x, y）を見つける言葉遊びも生み出されます（こういう言葉遊びを一般に「転文」と呼ぶのが、自分の中では定着しつつあります）。これを、並べ替えが1つでなく複数のときに考えるとどうなるでしょうか。

試しに、上記のSATOR畳文を定義している s と q とで考えてみましょう。s, q は図示すると次のとおりです。

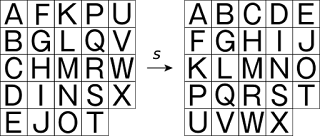
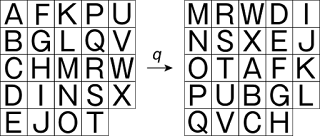
単純に考えると、「s(x)＝y」「q(x)＝z」となる文字列 x, y, z を見つければいい気がします。でも実はこれでは不満足です。というのは、SATOR畳文は、s と q とで変わらないだけではなく、「s してから q する」という並べ替え sq（次図参照）でも変わらないので、この並べ替えを仲間はずれにして考えるのは不自然だからです。sq(x)＝w となる w も同時に考えたい。

つまり、図中の文字を使っていえば

• x＝ABCDE FGHIJ KLMNO PQRST UVWX
• y＝s(x)＝AFKPU BGLQV CHMRW DINSX EJOT
• z＝q(x)＝MNOPQ RSTUV WXABC DEFGH IJKL
• w＝sq(x)＝MRWDI NSWEJ OTAFK PUBGL QVCH

という4つの文字列全部を考えるのが自然と思われます。この4つを見つけるのが、「SATOR畳文の転文版」ということになるでしょう。

面白いことに、SATOR畳文の転文版といえるのは、実はこれだけではありません。4つの文x, y, z, wのうち、いくつかが一致する場合を考えてみましょう。4つ全部が一致するのがSATOR畳文ですが、たとえば、全部は一致しないけれどxとyは一致する、というものを考えてみます。この場合、自動的にzとwが一致することがわかり、出てくる文字列は2種類になります。つまり

• s(x)＝x、q(x)＝z となる文字列 x, z を探す

という言葉遊びです。同様の言葉遊びはあと2つあって、

• s(x)＝y、q(x)＝x となる文字列 x, y を探す（x＝zの場合）
• s(x)＝y、q(x)＝y となる文字列 x, y を探す（y＝zの場合）

です。結果としては「SATOR畳文の転文版は4つある」ということになります。それぞれの場合の具体例は……誰か考えてください。

s, q 以外にも、いろんな並べ替えのいろんな組み合わせ方で、転文版を考えてみると面白いと思います。

(2) 清濁変換

ここまでに考えてきたのは、文字の「並べ替え」でした。文字の位置を変えるというものです。では、文字の位置を変えずに、文字そのものを変化させることを考えてみるとどうなるでしょう。

このような変換で、おそらく唯一面白くなるのが、「清音と濁音の変換」です。これを d と名付ければ、たとえば次のようになります。

d(かいぶん)＝がいふん
d(ぎょうざたべたい)＝きょうさだへだい

つまり、濁点がついている仮名からは濁点を外し、濁点がつけられるのについていない仮名には全部濁点をつける（いずれでもない仮名はそのまま）というのが d です。

回文などにならって、d で「変わらない」文字列を考えるのはたいして面白くありません。でも、転文のように、d で「移り合う」文字列を考えるのは面白いです。たとえば

d(がむ)＝かむ（ガム、噛む）
d(じゅーす)＝しゅーず（ジュース、シューズ）
d(なまこみた)＝なまごみだ（ナマコ見た、生ゴミだ）

などなど。清濁転文とでもよびましょうか。

d 単独ではなくて、回文を定義する p を d に組み合わせた変換 pd（つまり、文字列の前後をひっくり返したあとで d する）で変わらない文字列を考えるのも面白いです。これは、ひざみろさんにより提唱され青村豆十郎さんにより命名された「具対清濁」（具「体」清濁ではないので注意）という言葉遊びで、たとえば

はがぬけめもとれざんねんされどもめげぬかば
（歯が抜け目も取れ残念、されどもメゲぬカバ）

とかです。（注：ただし、ひざみろさんの考える具対清濁はどうやら中央の文字を例外視して考えることになっているようで、pd で不変にならない「いがい」「ぎせき」なども具対清濁と呼ぶようです。微妙に定義が違いそうなのでご注意を。）

d をほかの言葉遊び、たとえば縦横文と組み合わせるのも面白そうです。言葉遊びの可能性は無限大です！

おまけ：数学的に言うと

(1) 並べ替えが複数ある場合の転文は、数学的には、群論を使って説明するとクリアーになります。

引き続き、上記のSATOR畳文の例で説明します。並べ替え s, q で生成される群 G を考えます。G は位数4の群で、いわゆるクラインの4元群と同型になります。この G の任意の（正規）部分群 H に対して、次のような性質を満たす文字列の集合{x, y, z, ...}を探す、という言葉遊びが考えられます。

• x, y, z, ... はどれも H の任意の元で不変
• Gx＝{x, y, z, ...}（{x, y, z, ...}はGによるxの軌道になっている）

HとしてG全体を選ぶと、この言葉遊びはSATOR畳文となります。Gの部分群はほかに4つあり、それらがちょうど、上で説明したSATOR陣の転文版4つに対応するのです。

一般に、並べ替えからなる群 G が与えられると、その正規部分群ひとつひとつに対応して言葉遊びが考えられる、ということになります。たとえば、文字列の前後を入れ替える並べ替え p で生成される群 G の場合、Gは位数2で、その正規部分群は G と {1} の2つです。前者に対応する言葉遊びが回文、後者に対応するのがたいこめ、となります。これはとても面白いと思うんですが、面白いと思ってくださる方、誰かいませんか？


(2) 清濁変換については、文字の並べ替えと並列させて、次のように考えるとすっきりします。

文字列とは数学的に言えば、I＝{1,2,3,...,n}から、アルファベットの集合Aへの写像 f: I→A だと見なせます。そうすると文字の並べ替え t とは、定義域 I 上の全単射 t: I → I のことだと考えられます。たとえば並べ替え t を文字列 f に施すと ft（写像の合成）という新たな文字列になるわけです。他方で清濁変換のような、文字自体の変換 d は、f の値域 A 上の全単射 d: A → Aなので、その変換を文字列 f に施すと、df という形で d を左から合成した新たな文字列になります。

上で紹介した具対清濁というのは、dfp＝f となるfを探す言葉遊びなのです。


(おまけのおまけ) いろいろな言葉遊びに関して、文字列の並べ替えの群の構造を調べるのは面白いです。SATOR畳文の場合はクラインの4元群になると書きましたが、他の場合をいくつか書き並べてみると

回文、畳文、継母聞き耳	C2（位数2の巡回群）
畳回文、SATOR陣	V4（クラインの4元群）
畳文かつ2×2の左縦書き縦横文	D8（位数8の二面体群）
畳文かつ2×3の左縦書き縦横文	S4（4次対称群）
畳文かつ2×4の左縦書き縦横文	C2×A4（巡回群と4次交代群の直積）
2×3の左縦書きかつ右縦書き縦横文	(C2)^3とS3の半直積（輪積）

などとなり、それぞれに個性があります。興味ある方はさらに調べてみてください（そして教えてください。一般的に調べるのは私の手には負えなかった）。